What simply occurred? A gaggle of mathematicians created a “new” polygon beforehand identified to exist solely in idea. It is a 13-sided form that they dubbed “the hat,” despite the fact that it solely vaguely resembles one. What is exclusive about this geometrical determine is that it might probably tile a aircraft with out making a repeating sample.
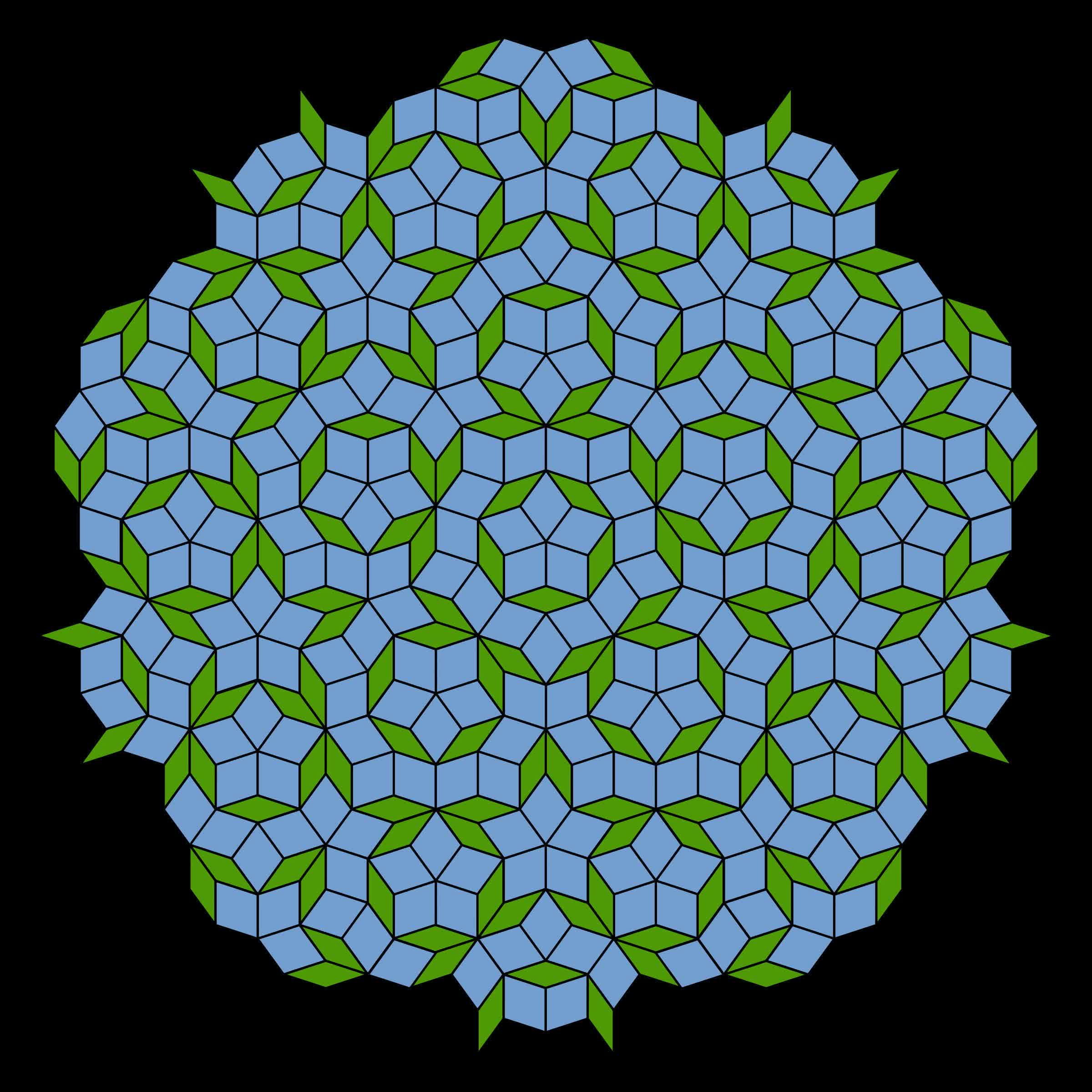
The hat can tile a floor with out creating transitional symmetry. In different phrases, the ensuing sample doesn’t repeat. It’s much like the Penrose configuration on this regard. At first look, you may see what you assume is a repeating sample, however take into account it extra carefully.
Think about a flooring lined in sq. or triangular tiles. You may elevate any part and match it on one other space as long as you do not rotate it. So there’s a transitional symmetry that repeats infinitely. The hat is a distinct chook.
Identical to the Penrose, you possibly can determine matching patterns on a small scale. Nonetheless, think about lifting that supposedly repeating collection of tiles and people round it and shifting them to overlay the opposite matching design—the smaller sample traces up as anticipated, however shifting farther from the similar sections exhibits the remainder of the structure doesn’t match.
The first distinction between the Penrose sample and the hat is that it solely requires one prototile as an alternative of two. This monotile is named an “einstein”—not named for the well-known physicist, however for the German phrase that means “one stone.” Sarcastically, the hat is definitely a polykite, that means that it was created from a number of kite shapes—particularly, eight kites related at their edges.
The existence of an einstein has for many years been purely theoretical. The mathematics proved it existed, however no person had discovered one till now.

“You are actually searching for like a one-in-a-million factor. You filter out the 999,999 of the boring ones, then you definately’ve received one thing that is bizarre, after which that is price additional exploration,” the research’s co-author Chaim Goodman-Strauss, a mathematician on the Nationwide Museum of Arithmetic, instructed New Scientist. “After which by hand, you begin analyzing them and attempt to perceive them and begin to pull out the construction. That is the place a pc can be nugatory as a human needed to be concerned in setting up a proof {that a} human might perceive.”
If you happen to’re concerned with all of the geeky math particulars, the researchers pre-published their paper on Cornell College’s arXiv repository. Additionally they have a devoted webpage with extra comprehensible layman’s info and pattern photographs relating to the elusive form.